Death by Fortran Common Block
After my 1995 summer-work at the Helsinki University Physical Chemistry Lab, professor Lauri Halonen gave me a full-time job as research- and teaching-assistant in the Lab in fall 1995. My attempts during the next three months to extend a Fortran molecular calculations program from 1972 provided ample challenges both in terms of science and software-architecture.
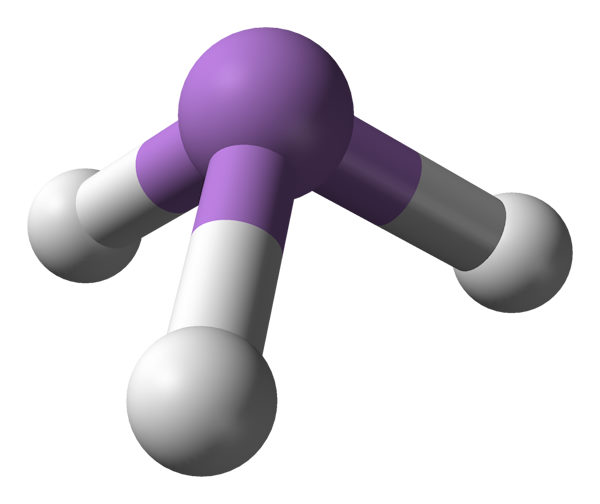
While the first summer-project was based on idea of Tuomas Lukka, the topic for the next one was provided by professor Halonen himself in a meeting at the lab on Monday 1995-09-18. The topic was to apply an anharmonic vibrational model to Arsine (AsH3) vibrations.
Arsine-molecule with Arsenic atom and three Hydrogens
Using experimental spectroscopic parameters of Arsine as input, I should determine Arsine vibrational potential energy surface as optimized parameters of a polynomial expansion in curvilinear coordinates. The calculation was to be done with a Fortran 66 program ANFF (ANharmonic Force Field) written 23 years earlier in 1972 by Aitken R. Hoy. Halonen gave me references for some related articles and books to read on the topic.
In my two years at the University, I had completed the basic Physical Chemistry courses, but not yet any of the advanced courses dealing with spectroscopy and molecular vibrations. So the self-learning curve on the project was quite steep.
Remote assistance 1990's style
I got a room that I shared with Janne Pesonen, a delightfully eccentric and inventive researcher who had formerly been studying History of Greek and Rome at the University, but decided later to switch from that to theoretical Physical Chemistry! Although Janne had also some insight into usage of the Fortran program, Halonen was by far the best expert on the topic in our lab and the go-to person for supporting and tutoring me in the project.
Hence it was particularly unfortunate, that just one week after our initial meeting Halonen flew to Princeton University for a one-year sabbatical to work on other projects. He of course wanted to support me remotely from USA as well, but this was early days of internet without video-calls and instant chats, before shared interactive documents and whiteboards - leaving vanilla email as the only feasible method for communication. This made the process of asking and providing advice and resolving problems occasionally frustratingly slow and clumsy. Although now 27 years later these emails (70 emails with about 60 pages of Finnish text in total) provide interesting written record of progress and challenges in the project and allow me here to summarize it below in English.
This main content of this article is clips from these project-emails, which relate to (1) theoretical framework and formulas for these molecular calculations (in particular to various molecular coordinates and their relationships), (2) Usage of thr ANHFF-program or Halonen that I was trying to carry out the desired calculations and (3) efforts to extend the program for larger number of parameters needed in the calculation.
For readers only interested in programming and not the scientific problems, consider skipping to chapter "Back to increasing array dimensions... and crashes"
Starting the project
In my first Emails to Halonen at Princeton is on 1995-10-02, about two weeks since his departure and shows still quite extensive open questions in my mind:
Date: Mon, 2 Oct 1995 19:12:55 +0200 (EET)
From: Robert Brotherus
To: Lauri Halonen
Subject: Topic of the Project
I have been reading the articles you provided (mainly A.R.Hoy et
al at the moment) and learning a lot, mainly about different molecular
coordinate systems and transformations between them (I did not know
that they play such an important role in the solution of the
vibrational-rotational problem!)
I am starting to take a look at the software, so I though it would
be good to re-iterate what actually was the topic and aim of the
project as out verbal discussion two weeks ago was quite brief.
- Determine arsine (AsH3) anharmonic potential energy surface as
expressed with coefficients of nth-order polynomial expansion.
Use curvilinear (geometric) coordinates.
- The initial values for the PE-surface coefficients are receive
from some Ab-Initio calculation (which?)
- The Fortran program you provided takes as input the coordinates
and their associated PE-coefficients and cross-coefficients and
some symmetry information.
- The program has two modes: direct and iterative. The direct one
calculates spectroscopic constants from the PE-surface.
The iterative mode optimizes PE-surface coefficients to match
spectroscopic constants.
For the optimization task, do I just need provide suitable input
for the existing software? Or do I have to modify the source code
of the software? Or do I have to write a different new software
that works together with your software?
[...]
Janne has been able to run the program and says it does calculate
correctly some spectroscopic parameters. He has been trying to
also make input-file for Arsine potential-surface but says there
are problems with some symmetry-related parameters.
From: Lauri Halonen (Mon, 2 Oct 1995)
Good that you contacted me so soon!
The initial potential-energy surface from article
Breidung ja Thiel, J. Mol. Spectrosc. 169, 166(1995).
Janne was supposed only to replicate the Beidung & Thiel results
for AsH3-molecule. You should now together check that the results
are valid. You were supposed to work with arsine too, later
use the iterative mode. As data points, we could initially use
alpha-coefficients which represent rotational constant
dependency on vibrational states, you can find these from literature.
Initial results - initial problems
Week later we have been able to carry out some calculations with Janne, but the results were mixed:
From: Robert Brotherus (Mon, 9 Oct 1995)
The confusion about input of symmetry information seems to have
been resolved and with Janne we have now input-file for arsine.
However, we did not find harmonic PE-parameters from
Breidung and Thiel article, so Janne used the ones
in Tuomas article instead.
The calculation produced results [...] But the results of g- and
x-constants are somewhat different from Breidung & Thiele values:
0 INDICES CONT2 CONT3 CALC. experim. calc.
1 1 -24.783 11.340 -13.442 -12.8 -10.88
1 2 20.934 -37.399 -16.466
1 3 -98.143 45.362 -52.777 -51.2 -43.28
[...]
From: Lauri Halonen (Tue Oct 10, 1995)
> we did not find harmonic PE-parameters
> from Breidung and Thiel article
The harmonic surface is in Thiels article (table XI), but it is
expressed in symmetrized form. With simple calculation it can be
converted to unsymmetric form [for the program input]. If you are
unable to to this, I will help. Tuomas and Juha Lummila have been
doing this in their papers, you can ask Juha for help.
> Our result are somewhat different [...]
Your results are different since you don't have Thieles 4th order
PE-parameters included in the calculation. I have sent email about
this to Janne already a while ago but he does not read his emails.
Can you ask Janne to be in contact with me?
I have written to Thiele and asked 4th order PE-parameters in
internal coordinate space. It might take some weeks before we
get that. Therefore you should focus on calculating the
alpha-parameters since they do not depend on 4th order surface.
Theoretical confusions and clarifications
The necessary conversions between the molecular force-field represented in internal and symmetric coordinates become of a topic of intense discussions, some misunderstandings and eventual clarifications:
From: Lauri Halonen (Wed, 11 Oct, 1995)
< Ok, I try to investigate to transformation from symmetry-coordinates
So the transform is:
S1 = (1/sqrt(3)) (r1 + r2 +r3)
S3a = (1/sqrt(6)) (2r1 + r2 +r3)
S3b = (1/sqrt(2)) (r2-r3)
So for example:
(1/2)F11*S1**2 + (1/2)F33*(S3a**2 + S3b**2) =
(1/2)frr*(r1**2 + r2**2 + r3**2) + frrp*(r1*r2 + r1*r3 + r2*r3)
Using these formulas you can derive relationship between
the F and f force coefficients.
From: Robert Brotherus (Thu, 12 Oct 1995)
> So the transform is: S1 = (1/sqrt(3)) (r1 + r2 +r3) [...]
Simple enough, though it's not clear to me why this specific linear
combination of coordinates is called "symmetry coordinates".
I try to interpret the Hoy et al article statement
"symmetry coordinates transform according to the irreducible
symmetry representations of the point group". While the symmetric
S1 does indeed seem to transform like A1 representation of
Arsines C3v symmetry group, but I don't see how the S2 and S3
would transform as the A2 and E representations of C3v.
From: Lauri Halonen (Thu, 12 Oct, 1995)
S1 transforms as A1. The pair (S3a,S3b) transforms as E (to the
other is Ea and other Eb). For bending-coordinates it goes in
same way, just replace r1 with theta1 and so on.
The terms Sa**2 and Sb**2 have indeed same coefficients
so that F3a,3a = F3b,3b. The cross-term F3a,3b * S3a * S3b
coefficient F3a,3b disappears for reason that I have been recently
describing to Janne, ask him. If it does not become clear, then ask me.
From: Robert Brotherus (Thu, 19 Oct 1995)
> Transform formula is: S1 = (1/sqrt(3)) (r1 + r2 +r3) [...]
> For example (1/2)F11*S1**2 + (1/2)F33*(S3a**2 + S3b**2) =
> (1/2)frr*(r1**2 + r2**2 + r3**2) + frrp*(r1*r2 + r1*r3 + r2*r3)
Does the example lack the term (1/2)F13*S3a*S3b on the left side?
Otherwise this transformation is now clear.
From: Robert Brotherus (Thu, 19 Oct 1995)
> The force-constant F(3a,3b) in the term F(3a,3b)*S3a*S3b vanishes due
> to reason that I have been recently explaining to Janne
But if this is so, how come Breidung and Thiel give a non-zero
harmonic symmetric force-constant in their paper:
i j
1 1 2.810
1 2 0.138
2 2 0.588
Why is F12 not zero above?
From: Robert Brotherus (Thu, 19 Oct 1995)
> F12 can be non-zero because both modes 1 and 2 are totally symmetric
> Do you understand this? Let me know if no.
I did not yet understand. I guess that my lack of understanding
is caused by different ways if indexing and naming.
Thiel is giving in his paper following symmetric force-constants:
i j
1 1 2.810
1 2 0.138
[...]
I understand this to mean stretch (1 symmetric, 2a ja 2b non-symmetric)
1 1 2.810
1 2a 0.138
[...]
And for bending: (3 symmetric, 4a and 4b non-symmetric)
3 3 2.839
3 4 -0.047
[...]
It seems that the coupling of stretch and bend vanishes because
those have not been marked anywhere?
When you give transform formulas like S3a = (1/sqrt(6) (2r1 - r2 - r3),
I assume that by S3a and S3b you mean same as Thiele with 2a and 2b
since Thiele uses 3a and 3b for bends and you are still
describing stretches.
You gave earlier an example which includes two symmetric stretch
related non-zero parameters (F11, F33) implying that others are zero,
yet Thiele gives three non-zero parameters (1-1) 2.810, (1-2) 0.138
and (2-2) 0.588. Which of those parameters are F11 and F33 and
that is the third one when it's not zero?
From: Lauri Halonen (Thu, 19 Oct, 1995)
You have got confused with the indexing of the coordinates and
parameters. That is quite understandable. I wish I could be there
to guide you in person. I am going to visit Helsinki 12-16.12,
lets talk then.
Both symmetry and normal-coordinates are indexed so that 1 is
the symmetric stretch (A1), 2 is the symmetric bend (A1), 3 (3a/3b)
is antisymmetric stretch and 4 (4a/4b) is antisymmetric bend. [...]
F12 can be of course non-zero because the product of Hamilton Operators
of symmetric stretch (A1) and bend (A1) is also A1 (A1 x A1 = A1).
F12 as a real number is naturally totally symmetric.
F13*S1*S3a is not totally symmetric (A1 x Ea = Ea).
F13 must be zero because that is the only to make this operator disappear.
Do not confuse this with the indexing of the non-symmetric
internal coordinates. These are r1, r2, r3, theta1, theta2, theta3.
These indexes have nothing to do wth indexes of symmetry coordinates.
I hope this starts to become more clear. I will help you if not.
From: Robert Brotherus (Thu, 19 Oct 1995, 21:47)
Lets try again:
Thieles MP2-level harmonic symmetric surface 1 is symmetric stretch,
2 is symmetric bend, 3 (a/b) non-symmetric stretches and 4 (a/b)
non-symmetric bends
i j
1 1 2.810
1 2 0.138
2 2 0.588
[...]
I need to convert these into force-field parameters in internal
coordinates. You told this can be done (for stretches)
with formula (1/2)F11*S1**2 + [...] = (1/2)frr*(r1**2+r2**2 + r3**2)
+ [...] Supposedly similarly for bends (1/2)F22*S2**2 + ...
I am greatly bothered by the lack of factors F12 and F34 in
these formulas. Can one really calculate the internal force parameters
despite throwing F12 and F34 to trash? This is difficult for me to believe.
My own guess for a proper conversion formula would be as follows:
1. Express the molecules potential-energy in symmetry coordinates
(omitting terms that are zero due to symmetry): (1/2)F11*S1^2+
(1/2)F12*(S1*S2)+... (Note that this formula includes F12 and F34)
2. Substitute in the formula symmetry coordinates with corresponding
expressions in internal coords eg. S1 = (1/sqrt(3)) (r1 + r2 +r3)
3. Expand and then collect together all r1^2 terms, all r1*r2 terms
etc and observe the expressions of force-constants that
come in front of these.
I must go to sleep
From: Lauri Halonen (Thu, 20 Oct, 1995)
> I am greatly bothered by the lack of factors F12 and F34 in
> these formulas [you gave for calculating stretches]
Note that the formulas I gave are only or a hypothetical problem which
only includes stretches. Of course additional terms are needed when
stretch is included!! I am sorry I did not express this
earlier clearly enough.
> My own guess for constructing the transform formula is as follows [...]
Exactly right!!
From: Robert Brotherus (Thu, 23 Oct 1995)
> Exactly right!!
Huh huh, finally, very good. Then the matter is exactly as I
originally thought, but my thinking was led to wrong path by
those example formulas ignoring bend.
I have been now going trough all Thieles cubic and quartic parameters,
collecting together ones that must be equal based on symmetry,
calculating averages etc and preparing input file for the program.
I trust that now I can finally get the harmonic parameters included
too and calculation going on.
Constructing the input for the program
1995 was time before invention of XML, JSON, YAML and other standard structured formats that we take nowadays for granted for moving and storing data. Input files for the ANFF-program like many other Fortran-programs of the time consisted of text files with plain untagged sequence of numbers, separated with whitespace. The meaning and usage of the number was determined only by its position in the sequence. Compared to the tagged formats of today, this was very brittle: a single missing or extra value in the middle of the file lead to subsequent numbers being assigned to wrong variables, leading to invalid calculation results or crashes.
Some of the input values represented the molecular potential-surface coefficients, but some represented configuration values for the program, like switches between different calculation modes. I brought up possibility to use symmetric coordinates in the calculation to avoid conversion to non-symmetric internal coordinates. Lots of back-and-forth resulted about which version of coordinates to use in the calculation. Fresh input from Walter Thiel from Switzerland seemed to tilt the case for internal coordinates.
From: Robert Brotherus (Thu, 12 Oct 1995)
I would be probably able to make the transform to non-symmetric
coordinates now, but it seems it might not be needed after all:
I noted that Breidung has both quadratic and cubic PE-parameters
in symmetry-coordinates. We are currently using internal coordinates
in the program input-file, but I have understood that it could also
be used with symmetry-coordinates. I am trying to make such input-file now.
From: Lauri Halonen (Thu, 12 Oct 1995)
Indeed, it seems that Thiel is giving results in symmetric form.
As I described earlier, these can be converted to unsymmetric form,
Juha Lummila can help with conversion formulas. It's not difficult
since I have succeeded in that as well.
But doesn't the program accept also input in symmetric form?
In that case the conversion is not necessary. Check this.
It might be that it accepts both forms.
From: Walter Thiel (Fri, 13 Oct 1995)
Dear Professor Halonen, 13 Oct 95
In the appendix we send you an internal quartic force field which
corresponds to a normal coordinate quartic field with phi(1234)=0.
[...]
Best regards Walter Thiel
AB INITIO VALENCE FORCE CONSTANTS FOR ARSINE AND STIBINE
1.) AsH3 Geometry: AsH 1.499706 Angstroms
HAsH 94.101882 Degrees
# F2INT ##
21
1 1 3.2406353648
1 2 .0015317068
1 3 .0015318780
[...]
# F3INT ##
56
1 1 1 -14.1924290409
1 1 2 -.0223750283
1 1 3 -.0223754492
[...]
From: Lauri Halonen (Thu, 14 Oct 1995)
I have forwarded you Thiels email with Arsine fourth order PE-surface
for arsine. This is in non-symmetric internal coordinates, check if
you can use this with the program or does it need to be converted to
symmetric form.
The harmonic surface cannot be taken from this Thiels email but
must be taken from his paper table IX because only that is accurate
enough. Since that is symmetric, it has to be converted to internal
coordinates to combine with the higher-order parameters in the email
or the higher-order parameters need to be converted to symmetric form.
Both are doable!
From: Robert Brotherus (Tue, 17 Oct 1995)
> But doesn't the program accept also input in symmetric form?
Yes, as far as I understand, the PE-surface can be given in internal
coordinates (along with suitable conversion-matrix) or in
symmetry-coordinates (in which case unit-matrix is given as
conversion matrix).
Our first input-file, which was done based on PE-surface in
Tuomas paper has internal-coordinate PE-surface and conversion matrix.
Breidun and Thiel use symmetric coordinates both in table 4 cubic
force-constants and table 11 harmonic force-constants, so I was
planning to make the input-file based on them. But now that I have
received Thiels email having all powers of parameters in internal
coordinates, I will use them after all. For symmetric transform
matrix we can probably use the same that we had in our initial input file.
> harmonic surface must be taken from his paper table IX
> because only that is accurate enough
Then I will try to convert the papers symmetric harmonic surface
to internal coordinates and combine with higher-order parameters
in the email.
Note also that the Thiel email contains much more cubic (56)
and quartic (126) force-field parameters than our input-file
based on Tuomas paper (26+9), in fact parameters are found
for all possible combinations of coordinates
From: Lauri Halonen (Thu, 17 Oct 1995)
Now compare the result: alpha- and x-constants. Note that our
program does not calculate alpha-constants 'correctly'
(difference is likely to be small compared to Thiele results.)
This is because our results include resonance coriolis -contribution
which is missing from the experimental results.
Later you will need to modify the program because of this.
From: Robert Brotherus (Tue, 17 Oct 1995)
Note that in Thieles list of force-constants, many should be identical
based on symmetry. Yet Thieles AbInitio -calculation naturally has some
random variation in them, for example:
f112 = -.0223750283, f113 = -.0223754492, f122 = -.0223783153.
For the force-field program, one should in such cases input the
value of the parameter only once and then refer to the parameter
three times. I propose that in such cases I will use as the value
of the parameter average from Thieles values, for example:
f112 = f113 = f122 = 1/3 * (-.0223750283 -.0223754492 -.0223783153)
From: Lauri Halonen (Tue, 17 Oct 1995)
Exactly so!
From: Janne M Pesonen (Tue, 17 Oct 1995)
> Can you borrow me the diagram about how you had been numbering
> Arsine atoms and vibrations for the input-file? Alternatively
> I can develop a way of numbering myself.
Yes, I will bring the diagram tomorrow.
I can leave on your desk if you are not there.
The revenge of bad results
Around 23.10 I was optimistic that the extensive challenges in forming input file for the program were resolved and I could finally get some valid results. Unfortunately the optimism proved to be unwarranted and problems just starting
From: Robert Brotherus (Tue, 24 Oct 1995)
Subject: Calculation finally executed
I was finally able to convert the symmetric PE-surface to internal,
combine those with the new cubic & quartic parameters,
construct input file and execute the calculation.
[...]
But the calculation results seem completely different from
ones in the Thiele article. For example:
X-constants Calc Thiele
1 1 18.437 -10.88
1 2 148.114 -2.06
1 3 19.333 -43.28
[...]
Well, so different results probably cannot be explained just by my
using of slightly different surface? I guess I need to re-check the
validity of the input file once more.
From: Lauri Halonen (Tue, 24 Oct 1995)
There must be some flaw in the input file!
I will help if needed
From: Robert Brotherus (Thu, 26 Oct 1995)
First I noted, that the indexing that Janne had used for bends did not
correspond to the indexing by Thiele. Because I had copied the
U-symmetrizing matrix from Jannes input file, that lead to errors.
I fixed this by swapping in Thieles data bend indexes 4 and 6 from
force-field parameters of all order.
I figure the harmonic constants I calculated are ok after all:
although they are significantly different from Thiele SCF-surface,
they match very well with Jannes input file (from Tuomas).
But then I noticed problem in the output of of cubic parameters:
Althought my input file has:
1 1 1 1
2 2 2 1
3 3 3 1
1 1 2 2
...
Yet the printout shows:
INPUT FORCE CONSTANTS (CUBIC)
1 1 1 4 -0.0029
2 2 2 6 -0.2033
3 3 3 4 -0.0029
1 1 2 4 -0.0029
1 1 3 5 -0.014
...
So program is combining terms to wrong force-parameters!
This of course causes the input to be completely incorrect.
With Jannes input this problem does not occur. I have not yet
identified cause of this problem, but the only significant
difference in this new input set I can think of is the much
bigger number of parameters. Problem is not present in quartic
terms and even in cubic terms it only occurs in 15 of them.
From: Lauri Halonen (Thu, 26 Oct 1995)
I do not easily believe that the program has some error.
Doesn't Janne have same number of cubic force-field parameters as you?
Hint: run the program with cubic parameters only (you cannot calculate
x-constants then). Check if there are indexing mismatches then.
Janne has been testing the program with CHF3, look at that,
is indexing ok there? As a last resort we can look at the Fortran-code
itself. Any mistakes in indexing must happen quite close to the beginning,
so it should be easy to find.
Increasing array sizes should be simple, right? Wrong
After extensive troubleshooting, it turned out that the number of parameters in my model was too much or the fixed-size arrays of the Fortran program. I got some reservations about trying to modify the program since it was a complex mess of code in single file of 8000 lines
From: Robert Brotherus (Thu, 12 Oct 1995)
Do you have any more specific description or documentation about
the program, bit like the one of the "Tetra" software of Child
and you? I have been investigating the source-code a bit,
but it is so messy (no indentation, lots of goto-jumps and bad
programming style) that I will not be able to get much wiser
from that any time soon.
From: Lauri Halonen (Thu, 12 Oct 1995)
The anharmonic force-field program is unfortunately difficult to
understand. Only documentation is the usage explanation text.
It has some comments.
The nasty aspect of Fortran is that is is difficult to program without
using GOTO-statement. Because of that my programs are bit difficult to
understand. On the other hand, for us the most important thing is to get
correct results. Cosmetic matters are not critical.
So most important is that the program works correctly.
From: Robert Brotherus (Tue, 17 Oct 1995)
> Cosmetic matters are not critical.
I understand. Although it would be nice to also understand how
the program is calculating in addition of getting correct results.
But perhaps that can wait for later.
I nevertheless got to work to increase the size of those arrays, thinking it would be a simple matter. But such optimism soon proved unfounded.
From: Robert Brotherus (Fri, 27 Oct 1995)
I found the error and it is indeed related to the number of
force-parameters. Janne has only 30 parameters (21 cubic, 9 quartic)
whereas my model has 56 + 126 parameters, all possible combinations.
The errors arise from the fact that the program supports maximum of 100
parameters of each kind. When I removed 30 quartic parameters from the
end of the list (making their number 96), I started to get quite nice
results:
i j Janne Thiele Experim My new calculation
1 1 -13.44 -10.88 -12.80 -16.92
1 3 -52.78 -43.28 -51.20 -65.33
...
I could try to change the program to accept more parameters.
From: Lauri Halonen (Fri, 27 Oct 1995)
How do you know that you can input maximum of 100 parameters of each kind?
Did you look at the program code?
You have been entering the unsymmetric field. There are many parameters
that are identical due to symmetry. Do they all need to be entered there?
We can enter all in symmetrized form. It requires some additional work!
Alternatively you can modify the program. Symmetrization happens probably
close to the beginning of the code. Probably not impossible to adjust the
dimensions of the arrays there.
From: Robert Brotherus (Mon, 30 Oct 1995)
I am trying to modify the program: I found from two locations
(the input-routine and symmetrization-routine) table for F3 and F4
constants, which both have size 100. I increased the indexes to
200 and recompiled the program. The program is now able to read in
all 56+126 parameters, but then crashes in middle of calculation.
I continue to investigate cause of the crash and try make it work.
Crash seems to happen in part where program tries to print out
U-matrix for symmetrizing the parameters.
I need to consider once more using symmetrized input if I cannot
get the program array fixes done.
From: Lauri Halonen (Mon, 30 Oct 1995)
Good that you have started to look how to fix the array dimensions.
Note however, that such changes need to be done in all relevant
locations so it can be a bit difficult task. [...]
From: Robert Brotherus (Thu, 2 Nov 1995)
I found only two locations containing the array maximum index 100:
the input- and symmetrization routines, as one might expect.
Nevertheless increasing the indexes to 200 crashes the program.
From: Lauri Halonen (Thu, 2 Nov 1995)
Why does it crash in symmetrization? The part of the program that
handles symmetrization can't be more than few lines long.
Isn't any error in that easy to find?
From: Robert Brotherus (Fri, 3 Nov 1995)
It's indeed weird that the program crashes after increasing the array
sizes. I have not used much time now to investigate that further and
pursued the alternative of using symmetric coordinates instead.
One more try with symmetric input
With the increased array-dimensions leading to mysterious crashes, I switched once more to the idea of converting all parameters to symmetric form. This would result in smaller number of parameters, presumably fitting to the limit 100 of the program.
From: Robert Brotherus (Thu, 2 Nov 1995)
As a backup solution, I tried to make with C a small program
for converting the parameters to symmetric form, but it is
not calculating correctly. For example for harmonic parameters
I calculate now:
F(a,b) = (sum over i and j) f(i,j)*(U(i,a)*U(j,b)+U(i,b)*U(j,a))
What's wrong with this?
From: Robert Brotherus (Fri, 3 Nov 1995)
I got my symmetrization C-program to finally work. I wasted a lot of
time because I used mistakenly wrong indexes internal harmonic surface:
normally I have bend 6 opposite of stretch 1, but now I had it other
way round which lead to wrong value for parameter 3 4.
I will now try to extend that to te cubic and quartic terms.
From: Robert Brotherus (Tue, 7 Nov 1995)
Now I think my c-program for calculating symmetric parameters works.
I will run the calculation tomorrow. However, I am concerned about one
thing: my calculation is giving non-zero values to some parameters
that should be zero based on symmetry. Is it ok that I just remove them
afterwards - or should this happen at all? At least for harmonic
parameter the conversion is calculated correctly.
From: Lauri Halonen (Tue, 7 Nov 1995)
Unfortunately this still sounds bit bad. There must not be any
non-zero parameters that should be zero from symmetry!
This can have two reasons:
1. Your C-program has still some error
2. The non-symmetric source-parameters calculated with ab-initio
have slight errors and therefore will not cancel each other completely.
(But the resulting values should still be very close to zero.)
How much do these parameters differ from zero?
From: Robert Brotherus (Thu, 9 Nov 1995)
Janne also agrees that there should not be any non-zero parameters
that are zero by symmetry. The weird thing is that the program still
calculates correctly the non-zero harmonic parameters (I get back
the same symmetric parameter from which I calculated the non-symmetric
ones few weeks ago).
Here are the calculated symmetric parameters:
1 1 2.810000
1 2 0.138340
1 3a 0.01366 [should be zero]
[...]
So some parameters that should be zero are zero, some are not.
Here is my code for the harmonic parameters:
for (a=1; a<=6; a++) for (b=a; b<=6; b++)
{ force = 0.0;
for(i=1; i<=6; i++) for(j=1; j<=6; j++)
force += NonSym2[i][j] * ( U[a][i] * U[b][j] ); }
As far as I understand, the U matrix should be valid too.
Indexing could be a potential problem. But I have been aiming
to use same indexing to stretches and bends as you and Janne.
Thiele is using in his surface different indexing,
and I have had to swap his indexes 4 and 6.
But I don't see any problem here.
Janne promised to repeat the calculation with MathCad so we can
see how the results differ. Pity that the project progress
is currently stalled in this kind of small thing.
From: Lauri Halonen (Thu, 9 Nov 1995)
I started to also wonder what the problem is. I wrote a small fortran
program that does the same calculation for harmonic parameters.
The program works ok.
[...Fortran code for the program ...]
Note that Thiele indexing must be adjusted: [...]
I hope this helps. I help more if needed.
From: Robert Brotherus (Thu, 9 Nov 1995)
For indexing I have indeed changed everywhere 4 <==> 6.
It's difficult for me to think what kind of bug in my program fail to
produce some zero-values correctly and yet provide all non-zero
values correctly.
I will look more closely tomorrow to the program code you sent.
But the core calculation looks quite much like my own.
From: Robert Brotherus (Thu, 16 Nov 1995)
I was few days ill, now back working.
Symmetrization calculation works now. The bug in my program was
that is was missing the part that copies the force-field matrix
parameters from one side of the matrix to the other.
In your program this was:
DO 8 I=1,6
DO 9 J=I,6
F(J,I)=F(I,J)
The confusing aspect of this bug was that it had only very
small effect on the results (in 5th decimal places) which made
the non-zero parameters look correct on the first glance.
I added now this missing part and corresponding tensor parameter
mirroring for cubic and quartic force-field values.
From: Robert Brotherus (Mon, 20 Nov 1995)
Symmetric input parameters seem to be calculated okay now.
There are now 26 Cubic parameters (with 18 different values)
and 62 quartic parameters (with 42 different values).
Now, however, we are blocked by another array-size limitation in
the program: we have now 60 independent force-field parameters
(cubic & quartic), but the program only accepts 50. (Last time
with the non-symmetric input the problem was that there was more
than 100 quartic parameters, now there are only 62)
I will see if this time I will succeed in increasing the program
array size limitation.
Back to increasing array dimensions... and crashes
Having exhausted all options to reduce the number of force-field parameters enough for the programs array-size limitations, there was not other way than to determine why increasing those limitations lead to crashes. The crashes themselves did not provide much data to work on: the process simply terminating mid-execution with no error messages or hint of cause.
From: Lauri Halonen (Mon, 20 Nov 1995)
Now there remains no other solution but to fix the program to allow more
parameters. Terms cannot be discarded, idea is to use the whole
Ab Initio surface.
From: Robert Brotherus (Tue, 23 Nov 1995)
The program manual states the maximum number of different force-field
parameters to be 50 (we have 60). I searched the whole source-code for
instances of the constant 50 and found many from both main program an
various subroutines: FIND(50), FREF(50), JWE(50), JAC(200,50), etc.
I changed all instances of 50 to 100. I am currently trying to
re-compile the program: compiler reports several syntax errors
but without line numbers, so they are slow to find in Emacs.
From: Robert Brotherus (Mon, 27 Nov 1995)
My attempts of increasing array maximum indexes in the program are not
going well. As noted, to allow more than 50 force parameters, I have
changed all maximum dimension 50:s in the code to 100, for example:
COMMON POSV(7,3),U(20,20),U1(20,20),Z(50,50),FIND(50),FREF(50),...
=> COMMON POSV(7,3),U(20,20),U1(20,20),Z(100,100),FIND(100),FREF(100),...
Common sense would imply that increasing such array dimensions can never be
a bad thing: extra space should do no harm even if it is not used.
Yet the program with these modifications crashes to seemingly
random Division By Zero or OS Errors:
*** Floating Point Exception: Floating divide by zero: at 80020f9c
...
Same errors happen even if I only increase dimensions of
the 1-dimensional arrays of size 50:
FIND(50), FREF(50), JWE(50), DF(50), PD1(50), PD2(50), ...
=> FIND(100), FREF(100), JWE(100), DF(100), PD1(100), PD2(100), SCL(100),
After investigating the program I have determined the FIND-array
to be the one containing cubic and quartic force-field parameters.
But the program crashes even if I only change the
first FIND(50) to FIND(100)!
As a person with experience on Fortran, do you have any comments
of this extremely weird error? This seems to be the exactly same
error that appeared month ago when I was trying to input unsymmetric
force-field parameters (126 of them) and increase size of another
array from 100 to 200. Those errors were the reason we tried to
switch to use the symmetric parameters, but that does not help
at all if even this other array sizes cannot be increased.
Horrors of the Fortran Common Block revealed
The answer of the mystery-crashes was finally revealed... and the reason proved to be a very disturbing one for any software architect.
From: Lauri Halonen (Wed, 27 Nov 1995)
You are right that increasing the array dimensions is allowed
in principle. But when one does that, one needs to be very careful.
One must update relevant indexes throughout the entire program.
Note especially, that subroutines can use different name for the same
variable. The subroutines need to declare same dimensions for same
variables even when they have different names. For example:
Main program statement: COMMON /ROBERT/ A(100),B(30,4)
Subroutine statement : COMMON /ROBERT/ D(100),E(20),F(100)
If you now change in main program A(200), you need to adjust also
subroutine array dimensions. Most likely you need to change to D(200)
but there are other possibilities. The program might be also using
EQUIVALENCE-statements to use same memory area for different variables.
That can also cause trouble when changing array dimensions.
From: Robert Brotherus (Mon, 28 Nov 1995)
Ok, I start to now understand the logic of Fortran COMMON-statement:
in COMMON /ROBERT/ the name ROBERT refers to specific memory location
and different subroutines can declare to treat that memory with collection
of any variables they choose. The mystery was now solved when I inspected
the different COMMON-block definitions of different subroutines. For
example two different subroutines of the program define:
Subroutine A:
COMMON POSV(7,3),U(20,20),UU(20,20),DUM1(2720),B(15,20),...
Subroutine B:
COMMON POSV(7,3),U(20,20),U1(20,20),Z(50,50),FIND(50),FREF(50),F2(120),...
Here Subroutine A contains a "dummy" array DUM1(2720) in the same memory
area which Subroutine B contains Z(50,50), FIND(50), FREF(50), F2(120).
Note that 50*50 + 50 + 50 + 120 = 2720. So to change FINT(50) => FIND(100),
one needs to change all DUM-arrays in all subroutines in corresponding way.
One one hand I am relieved that this nasty mystery is finally understood.
On the other hand I am shocked that any program / programming language uses
such archaic ways. If I would have done this program, increasing the
dimensions would require changing exactly one number and require 5 seconds.
Nevertheless, I will proceed in a new attempt to increase the dimensions
and hope to get then valid calculation results with the full parameter set.
So the horrible revelation was out. If one want to change FINT(50) array to be FINT(100), it is not enough to search and fix the source-code for all arrays with dimension 50. One also needs to:
- Search all subroutines COMMON-block definitions for all dummy-arrays
- Determine which dummy-arrays contain the same memory-area as FINT by comparing them to COMMON-block definitions of all other subroutines
- For dummy-arrays determine to contain FINT, calculate the formula for their total size
- Determine how the formula is affected by the changing of the FINT and adjust the dummy-array dimensions accordingly.
If one neglects to correct the dimension of DUM1(2720) - or any other of the numerous similar dummy-array definitions (or makes any mistake in changing it), instead of helpful compilation error message the subroutines just operate on wrong memory area and program crashes in random and violent ways.
From: Lauri Halonen (Tue, 28 Nov 1995)
Your critique [of the common-block / dummy-array architecture] is not
completely appropriate, because current version of Fortran-language allows
use of variables instead of plain numbers for array dimensions.
Using those it would be indeed 5 second work to change the dimensions.
But take into account, that this ANFF-program has been written around
year 1972. Were you even born then? I had just graduated from high-school
and had never used any computer. I was not even aware of any computer
languages. The good aspect of Fortran is that these old programs are still
usable. Same cannot be said from programs that have been written with
some other languages.
Unfortunately I also write programs with quite old style. However,
the main point is that the programs work correctly and are fast.
I have understood that Fortran-compilers produce quite efficient code.
This ANH-program has been written in England an is somewhat
difficult to understand.
You should read the article:
Aitken R. Hoy, Mills, Strey Mol. Phys. 24, 1265 (1972).
I was indeed not born yet in 1972 when ANFF-program had been written by A. R. Hoy, only in 1973. I found the article abstract online and it describes calculations for "The relationship of the anharmonic force constants in curvilinear internal coordinates to the observed vibration-rotation spectrum of a molecule is reviewed. [...] Sample calculations on the water and ammonia molecules are reported."
More COMMON-block variables, more problems
Then it turned that the dummy-array adjustment for FIND and FREF was only the tip of the iceberg, with several other variables also dependent on the number of force-field parameters...
From: Robert Brotherus (Wed, 29 Nov 1995)
To my horror, I noticed now that FIND and FREF are not the only arrays
where the limitation of 50 parameters applies. For example there is code:
DO 401 I=1,NFIND
READ (IN,*) (Z(I,J),J=1,NFREF)
This seems to indicate that Z-array dimensions need to be similarly
extended (NFIND is the number of different force-field parameters).
From: Robert Brotherus (Thu, 30 Nov 1995)
I have now updated all Z(50,50) dimensions to Z(100,100) and located
from all subroutines all affected DUM1(...), DUM2(...), etc dummy
arrays, re-calculated new dimensions for all of them.
But it is difficult to say if even further array-dimensions would need
adjustment. After adjusting Z-matrix, the program still contains many
arrays containing the number 50 in the dimension, such as JAC(200,50),
JWJ(50,50),JWE(50),DF(50), PD1(50),PD2(50),PDEV(50,50) and SCL(50).
Some of them might be related to the number of force-field parameters,
but many surely do not, since the input-file defines also additional
input-arrays that have limitation of 50 values.
It if difficult to determine the connections between various arrays,
since the program is 8000 lines long (about 160 A4 pages), contains more
than 30 subroutines with COMMON-blocks and any statement in any subroutine
can create an implicit connection between variables. The subroutines use
variety of names for same variables and variety of different dummy-arrays.
I will therefore need to assume that all arrays with dimension 50 are
related to force-field parameters and start increasing their dimensions to
100 one-by-one with the associated dummy-array adjustments. I hope that
will finally help.
From: Lauri Halonen (Thu, 30 Nov 1995)
In the list of variables you wrote, at least JWJ and JWE dimensions are
related to the number of force-field parameters. These are used in the
least-squares calculation (which you are not utilizing at the moment).
The expansion of the relevant program dimensions might now require more
close investigation and understanding of the program. Try to do that
yourself and if that does not succeed, I will take a look.
At this point I was summarizing the challenges of the project to my USA family friend, professor Hayes Griffith:
To: Hayes Griffith @ University of Oregon
From: Robert Brotherus (Thu 30 Nov 1995)
Subject: Research
Hi Hayes! I apologize for not having sent you and deb some photos yet.
But that's on my task list and will be done sooner or later.
Just after arriving back to Finland my physical chemistry professor
offered me a job as a research / teaching assistant and that's what
I've been doing for the term in addition to my studies.
The teaching part - mostly guiding the labwork of younger students -
has been very nice and rewarding.
The research has been more problematic for several reasons.
The aim of the project is to improve the calculations of
rotation-vibration wavefunctions for arsine-molecule (AsH3) using
a combination of variational and perturbation theory. The biggest
challenge is that my professor has been all this time in USA
(will return in Sep 96) and all our communication must have been
through email. That's of course better than letters but has drawbacks
compared to direct discussions. The project is purely theoretical
one and I'm basically doing it alone.
Second, I still haven't been able to take some of the theoretical
chemistry courses that would help in this - my professor will lecture
them after coming back to Finland. Meanwhile, I have to learn necessary
theory from reading articles alone and this has proven to be
time consuming.
Third, the calculation we are planning uses partly a fortran program
written by someone in England 23 years ago (before I was born!).
The program is 8000 lines long, there is no documentation,
no comments in the program, it's written in a bad programming style
(lot's of gotos, bad variable names, common-areas with dummy-variables,
etc), and I have never programmed in fortran.
Fourth, I am also taking normal courses and doing the teaching
part of the job so that I have not been able to devote many hours
of day to the project although I have worked long hours and made
compromises with hobbies.
The project was supposed to start with a minor modification to the
program which would extend its capabilities to the calculation of arsine.
Due to the complications stated above the program still doesn't work
well for AsH3 and I am still working on the modification.
From: O. Hayes Griffith (18 Dec 1995)
I can well understand your frustration in research [...] I think you
should not continue too long on this project.
Switching project
It was probably clear to professor Halonen at this point that my mental endurance was wearing thin, so discussion about trying out a different project was started ahead of his visit to Helsinki in the christmas holiday. This was agreed in the end.
From: Lauri Halonen (Thu, 07 Dec 1995)
How are you doing Robert? I am Helsinki for one week starting 12.12.
I would like to then discuss with you as soon as possible.
Let's look at this project together. I was wondering if we should do
something different and then continue this project later when I am
back in Finland. We could surely think of some nice Thesis article
topics. This current project is more suitable later as a PhD project.
You can in the spring term continue in the lab assistant position,
so work will continue.
From: Robert Brotherus (Fri, 08 Dec 1995)
I was this week focusing on reading to exams. Today were exams in
Organic Chemistry and Kinetics. Because I had missed some lectures
due to the lab assistant work I needed to read bit more before the
exams, which went well in the end.
Let's indeed discuss when you are in Helsinki. It's not bad idea to put
this project on hold for a while. Unfortunately so far this project has
contained 80% of debugging and fixing computer programs and only
20% physical chemistry. Although I have still learned a lot.
A project change was then indeed agreed, as I describe to my USA professor friend:
To: Hayes Griffith @ University of Oregon (Wed Dec 27)
Things have actually improved in some aspects even before I received
your mail. My professor / advisor visited Finland for one week before
christmas and we decided to change my project. We planned to continue
with the original project at some lated date when he is back in Finland
and can better help me. The problem in last term has not been that
Dr. Halonen would not have interest in the project or that he would not
have been helpful - on the contrary. The problem has simply been his
absence and the lack of other people in the department that would have
had specific knowledge about the problems in this project.
The new project is much more straight forward - rotational analysis
of an infrared spectra of a linear molecule. What comes to advice,
things are not much better, because my new adviser Dr. Vaittinen is
ALSO leaving abroad soon (!). But he has taught me theory and practice
about the analysis in the past week and I feel I am now quite
self sufficient.
An improving factor is that there are 2 other people in the
department I know that have been doing similar analysis.
I should be able to talk with them when problems occur.
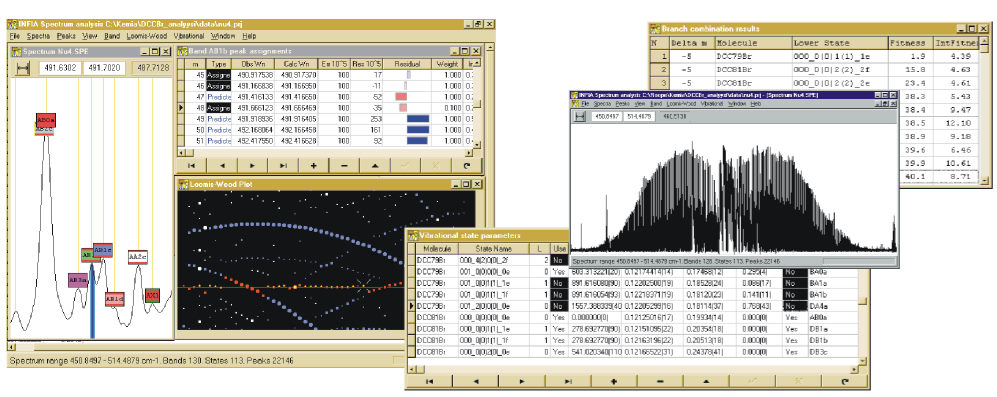
The project-switch eventually lead to my successful development of Infia Spectrum Analysis software which become the main topic of my Master Thesis as well as Licenciate degree.)
Reflection in 2024
We had planned with professor Halonen to proceed with full variational vibrational analysis of the Arsine-molecule by extending another Fortran-program he had written. The initial perturbation-theory calculation with the ANFF-program was supposed to be the initial "quick" step preceding the full vibration-rotation calculation. It was somewhat disappointing that after three months of struggling with various problems with the software, even the initial step was not completed. While we were able to agree on changing the project in the end (the next one leading to success with the Infia software), the failure to get significant process with this one did have an lingering negative impact on my self-esteem and enthusiasm related to Physical Chemistry.
Perhaps the combination of known up-front challenges - Halonen's trip in the USA, lack of local support, my lack of studies in advanced Physical Chemistry courses, my lack of experience with Fortran plus the low quality, complexity and lack of documentation of the ANFF program - should have made me request some easier project to start with instead of accepting this more ambitious project from Halonen. Especially considering that I had already had the earlier summer-work project grinding down in a dead-end with no results except slowly increasing stress-level. But I was still too enthusiastic and optimistic to say no, especially when my lack of experience also meant that I was not aware of the biggest problems that were lurking behind the corner - the dreadful unknown unknowns - like the unbelievable complexity and brittleness of increasing array dimensions in a Fortran common-block architecture of ANFF program.
Regarding the steep learning curve on vibrational theory (especially related to the molecular coordinate systems, symmetry, force-fields and related transformations), it might have been more productive in the end for me to just read more books and articles on the basic theory instead trying to ask questions with email from Halonen with all the limitations of email. But that might not have been easy path either.
Finally, perhaps it would have been better for me to write ANFF-like software from scratch myself rather, with more modern tools and style. At least it would have been more educational than operating with the "black box" code of ANFF. At least I would have used techniques where increasing array sizes would not have caused catastrophic run-time failures. (With programming technologies available in 2024 I would never consider even having arrays that have any fixed maximum size.) Perhaps writing such program would have been slower in the beginning, but at least there would have likely been steady progress with the work, producing frequent small feelings of accomplishment, important for keeping mood and motivation high. And perhaps such approach would have been in the end faster in the medium term, with less technical barriers and better understanding.